Lab1-Part2_Music_Generation

EN

Google Colab

Introduction

ABC Notation: ABC notation

ABC notation is a shorthand form of musical notation using alphabetic characters a-g, A-G, and z to represent the corresponding notes and rests. It uses additional symbols to denote modifiers like sharps, flats, octaves, note length, key, and decorations. Originating from Helmholtz pitch notation and mimicking standard musical notation using ASCII characters, it facilitates online music sharing and provides a simple language for software developers. It differs from other symbols designed for convenience, such as fingerings and solfège.

ABC notation includes representations of notes, note lengths, key signatures, time signatures, etc. Here’s an example of ABC notation:

X:1
T:Alexander's
Z: id:dc-hornpipe-1
M:C|
L:1/8
K:D Major
(3ABc|dAFA DFAd|fdcd FAdf|gfge fefd|(3efe (3dcB A2 (3ABc|!
dAFA DFAd|fdcd FAdf|gfge fefd|(3efe dc d2:|!
AG|FAdA FAdA|GBdB GBdB|Acec Acec|dfaf gecA|!
FAdA FAdA|GBdB GBdB|Aceg fefd|(3efe dc d2:|!

The elements here are explained as follows:

• X:1 - This is the track number, indicating this is the first piece in the collection.
• T:Alexander's - This is the title of the piece, “Alexander’s”.
• Z: id:dc-hornpipe-1 - This is additional identification information, possibly a unique identifier in a database or collection.
• M:C| - This defines the time signature. C| indicates “Cut time” (or alla breve), a 2/2 time signature often used in fast marches.
• L:1/8 - This defines the default note length, here it is an eighth note.
• K:D Major - This specifies the key signature, D major.

The subsequent part is the main content of the piece, using specific symbols and letters to represent notes and rhythms:

• Bracketed numbers and letters, like (3ABc, indicate a triplet, meaning three notes played in the time of two.
• Letters represent notes, with uppercase letters indicating a lower octave and lowercase letters indicating a higher octave. For example, d and D represent the higher and lower octave of D respectively.
• | is used to indicate bar lines.
• : marks the end of a musical phrase, often used at the end of repeated sections.

The whole piece is a combination of these notes and rhythmic patterns, forming the melody of “Alexander’s”. It appears to be a fast-paced dance tune, possibly a hornpipe, a traditional dance form popular in Britain and Ireland.

Dataset

All datasets included in this experiment are from Irish folk songs, with over a thousand pieces all represented in ABC notation.

# Download the dataset
songs = mdl.lab1.load_training_data()

# Print one of the songs to inspect it in greater detail!
example_song = songs[0]
print("\nExample song: ")
print(example_song)

Found 817 songs in text

Example song: 
X:1
T:Alexander's
Z: id:dc-hornpipe-1
M:C|
L:1/8
K:D Major
(3ABc|dAFA DFAd|fdcd FAdf|gfge fefd|(3efe (3dcB A2 (3ABc|!
dAFA DFAd|fdcd FAdf|gfge fefd|(3efe dc d2:|!
AG|FAdA FAdA|GBdB GBdB|Acec Acec|dfaf gecA|!
FAdA FAdA|GBdB GBdB|Aceg fefd|(3efe dc d2:|!

We can try using library functions to play it

# Convert the ABC notation to audio file and listen to it
mdl.lab1.play_song(example_song)

From the introduction, we know that this notation includes note information as well as metadata like song title, key, and rhythm. How does the number of different characters in the text file affect the complexity of the learning problem? This will become important when we generate numerical representations for text data.

# Join our list of song strings into a single string containing all songs
songs_joined = "\n\n".join(songs)

# Find all unique characters in the joined string
vocab = sorted(set(songs_joined))
print(vocab)
print("There are", len(vocab), "unique characters in the dataset")

['\n', ' ', '!', '"', '#', "'", '(', ')', ',', '-', '.', '/', '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', ':', '<', '=', '>', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', '[', ']', '^', '_', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z', '|']
There are 83 unique characters in the dataset

We can see there are 83 unique characters that make up all the metadata.

Processing the Dataset

Let’s step back and think about our prediction task. We aim to train a Recurrent Neural Network (RNN) model to learn the musical patterns in ABC notation and then use this model to generate (i.e., predict) a new piece of music.

Specifically, we are asking the model: given a character or a sequence of characters, what is the most likely next character? We will train the model to perform this task.

To do this, we will feed a sequence of characters into the model and train it to predict the output, i.e., the next character at each time step. The RNN maintains an internal state dependent on previously seen elements, thus considering all characters seen up to the given point when generating predictions.

Vectorizing the Text

Before we can train our RNN model, we need to create a numerical representation for our text-based dataset. To do this, we will generate two lookup tables: one mapping characters to numbers and another mapping numbers back to characters. Recall that we just identified the unique characters present in the text.

### Define numerical representation of text ###

# Create a mapping from character to unique index.
# For example, to get the index of the character "d",
#   we can evaluate `char2idx["d"]`.
char2idx = {u:i for i, u in enumerate(vocab)}
print('{')
for char,_ in zip(char2idx, range(20)):
    print('  {:4s}: {:3d},'.format(repr(char), char2idx[char]))
print('  ...\n}')

# Create a mapping from indices to characters. This is
#   the inverse of char2idx and allows us to convert back
#   from unique index to the character in our vocabulary.
idx2char = np.array(vocab)
idx2char

We can print the contents of both

{
  '\n':   0,
  ' ' :   1,
  '!' :   2,
  '"' :   3,
  '#' :   4,
  "'" :   5,
  '(' :   6,
  ')' :   7,
  ',' :   8,
  '-' :   9,
  '.' :  10,
  '/' :  11,
  '0' :  12,
  '1' :  13,
  '2' :  14,
  '3' :  15,
  '4' :  16,
  '5' :  17,
  '6' :  18,
  '7' :  19,
  ...
}
array(['\n', ' ', '!', '"', '#', "'", '(', ')', ',', '-', '.', '/', '0',
       '1', '2', '3', '4', '5', '6', '7', '8', '9', ':', '<', '=', '>',
       'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', '

I', 'J', 'K', 'L', 'M',
       'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z',
       '[', ']', '^', '_', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i',
       'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v',
       'w', 'x', 'y', 'z', '|'], dtype='<U1')

At this point, we have provided a unique integer representation (our vocabulary) for each character, where each character is mapped to an index from 0 to len(unique).

Now let’s implement the conversion of all song strings into vectorized (i.e., numeric) representations.

### Vectorize the songs string ###

'''TODO: Write a function to convert the all songs string to a vectorized
    (i.e., numeric) representation. Use the appropriate mapping
    above to convert from vocab characters to the corresponding indices.

  NOTE: the output of the `vectorize_string` function
  should be a np.array with `N` elements, where `N` is
  the number of characters in the input string
'''

def vectorize_string(string):
  output = [char2idx[char] for char in string]
  return np.array(output)
  # TODO

vectorized_songs = vectorize_string(songs_joined)
vectorized_songs

array([49, 22, 13, ..., 22, 82,  2])

We can also see how the first part is mapped to integer representations

print ('{} ---- characters mapped to int ----> {}'.format(repr(songs_joined[:10]), vectorized_songs[:10]))
# check that vectorized_songs is a numpy array
assert isinstance(vectorized_songs, np.ndarray), "returned result should be a numpy array"

nT:Alex' ---- characters mapped to int ----> [49 22 13  0 45 22 26 67 60 79]

Creating Training Samples and Target Sequences

Our next step is to divide the text into sample sequences used in training. Each input sequence to the RNN will contain seq_length characters from the text. We also need to define a target sequence for each input sequence, used to train the RNN to predict the next character. For each input, the corresponding target will contain the same length of text, shifted one character to the right.

To do this, we will split the text into chunks of seq_length+1. Assuming seq_length is 4, and our text is “Hello”. Then, our input sequence is “Hell” and the target sequence is “ello”.

The batch method will allow us to convert this stream of character indices into sequences of the desired size.

### Batch definition to create training examples ###

def get_batch(vectorized_songs, seq_length, batch_size):
  # the length of the vectorized songs string
  n = vectorized_songs.shape[0] - 1
  # randomly choose the starting indices for the examples in the training batch
  # np.random.choice(a, size): This function randomly selects `size` numbers from 0 to `a-1` (including 0 but not `a`). Here, `a` is `n - seq_length`, and `size` is `batch_size`.
  idx = np.random.choice(n-seq_length, batch_size)

  '''TODO: construct a list of input sequences for the training batch'''
  input_batch = [vectorized_songs[i : i+seq_length] for i in idx]# TODO
  '''TODO: construct a list of output sequences for the training batch'''
  output_batch = [vectorized_songs[i+1 : i+seq_length+1] for i in idx]# TODO

  # x_batch, y_batch provide the true inputs and targets for network training
  x_batch = np.reshape(input_batch, [batch_size, seq_length])
  y_batch = np.reshape(output_batch, [batch_size, seq_length])
  return x_batch, y_batch


# Perform some simple tests to make sure your batch function is working properly!
test_args = (vectorized_songs, 10, 2)
if not mdl.lab1.test_batch_func_types(get_batch, test_args) or \
   not mdl.lab1.test_batch_func_shapes(get_batch, test_args) or \
   not mdl.lab1.test_batch_func_next_step(get_batch, test_args):
   print("======\n[FAIL] could not pass tests")
else:
   print("======\n[PASS] passed all tests!")

[PASS] test_batch_func_types
[PASS] test_batch_func_shapes
[PASS] test_batch_func_next_step
======
[PASS] passed all tests!

For each of these vectors, each index is processed at a single time step. Therefore, for the input at time step 0, the model receives the first character’s index in the sequence and tries to predict the next character’s index. At the next time step, it does the same, but the RNN also considers the updated state from the previous step, i.e., its updated state.

We can better understand this process by seeing how it works in the first few characters of our text:

x_batch, y_batch = get_batch(vectorized_songs, seq_length=5, batch_size=1)

for i, (input_idx, target_idx) in enumerate(zip(np.squeeze(x_batch), np.squeeze(y_batch))):
    print("Step {:3d}".format(i))
    print("  input: {} ({:s})".format(input_idx, repr(idx2char[input_idx])))
    print("  expected output: {} ({:s})".format(target_idx, repr(idx2char[target_idx])))

Step   0
  input: 22 (':')
  expected output: 48 ('W')
Step   1
  input: 48 ('W')
  expected output: 60 ('e')
Step   2
  input: 60 ('e')
  expected output: 74 ('s')
Step   3
  input: 74 ('s')
  expected output: 75 ('t')
Step   4
  input: 75 ('t')
  expected output: 1 (' ')

The Recurrent Neural Network (RNN) model

Now we are ready to define and train an RNN model on our ABC notation music dataset, then use the trained model to generate a new song. We will train our RNN using batches of song snippets generated in the previous section.

The model is based on the LSTM (Long Short-Term Memory) architecture, and we use a state vector to maintain information about temporal relationships between consecutive characters. The final output of the LSTM is then fed into a fully connected Dense layer, where we apply a softmax over the vocabulary of characters and sample from this distribution to predict the next character.

The softmax function in this context refers to the activation function used in the output layer of the neural network. When training a language model (such as the RNN here), the softmax function is typically used in the final Dense layer to convert the LSTM layer’s output into actual probabilities.

Specifically, the softmax function:

1. Converts to probabilities:
   • It takes a vector of arbitrary real-valued numbers (such as raw outputs or logits from the Dense layer).
   • Then, it maps these values to a set of values between 0 and 1, such that the sum of all output values is 1, meaning each value can be interpreted as a probability. This is a normalization process.
2. Multiclass problems:
   • In a text generation task, each output corresponds to a character in the vocabulary.
   • The softmax ensures the output represents a probability distribution, where each character’s probability is based on the model’s prediction.
3. Sampling:
   • Once we have this probability distribution, we can sample from it to predict the next character.
   • The model will choose the character with the highest probability or randomly select a character based on the distribution to increase the diversity of generated text.

In my model, the output of the Dense layer at each time step goes through the softmax function, converting to probabilities for each possible character in the vocabulary. The model can then decide the most likely next character or randomly draw a character from these probabilities to generate text.

As introduced in the first part of this lab, we will use the Keras API, specifically tf.keras.Sequential, to define the model. The model will be defined with three layers:

• [tf.keras.layers.Embedding](https://colab.research.google.com/corgiredirect

or?site=https%3A%2F%2Fwww.tensorflow.org%2Fapi_docs%2Fpython%2Ftf%2Fkeras%2Flayers%2FEmbedding): This is the input layer containing a trainable lookup table that maps each character’s number to a vector with embedding_dim dimensions.

• tf.keras.layers.LSTM: Our LSTM network, with size units=rnn_units.
• tf.keras.layers.Dense: The output layer, with vocab_size outputs.

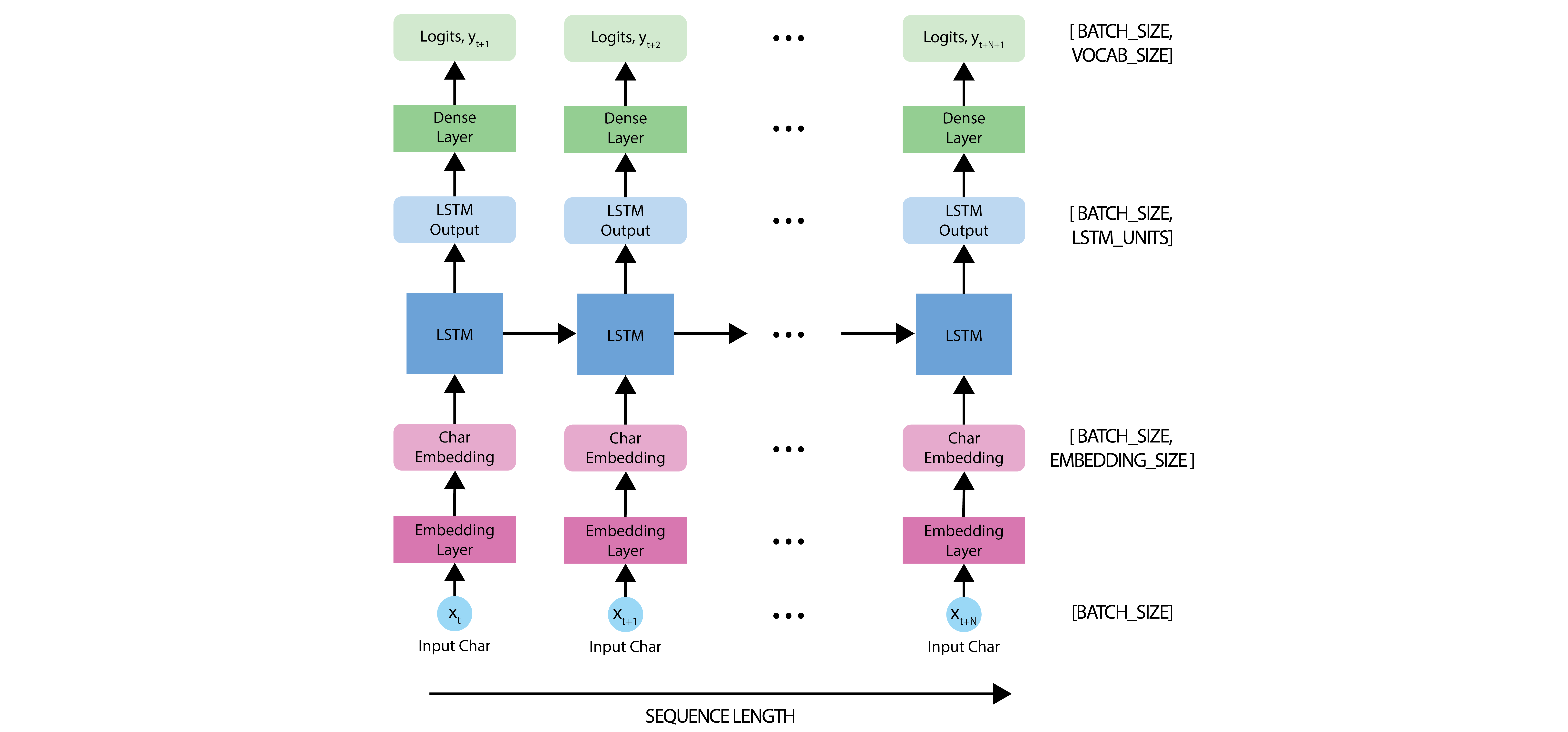
Now we will define a function to actually build the model.

def LSTM(rnn_units):
  return tf.keras.layers.LSTM(
    rnn_units,
    return_sequences=True,
    recurrent_initializer='glorot_uniform',
    recurrent_activation='sigmoid',
    stateful=True,
  )

It’s time to fill in the build_model function with the TODOs to define the RNN model and then call the function you just defined to instantiate the model!

### Defining the RNN Model ###

'''TODO: Add LSTM and Dense layers to define the RNN model using the Sequential API.'''
def build_model(vocab_size, embedding_dim, rnn_units, batch_size):
  model = tf.keras.Sequential([
    # Layer 1: Embedding layer to transform indices into dense vectors
    #   of a fixed embedding size
    tf.keras.layers.Embedding(vocab_size, embedding_dim, batch_input_shape=[batch_size, None]),

    # Layer 2: LSTM with `rnn_units` number of units.
    # TODO: Call the LSTM function defined above to add this layer.
    # LSTM('''TODO'''),
    LSTM(rnn_units),

    # Layer 3: Dense (fully-connected) layer that transforms the LSTM output
    #   into the vocabulary size.
    # TODO: Add the Dense layer.
    # '''TODO: DENSE LAYER HERE'''
    tf.keras.layers.Dense(vocab_size)
  ])

  return model

# Build a simple model with default hyperparameters. You will get the
#   chance to change these later.
model = build_model(len(vocab), embedding_dim=256, rnn_units=1024, batch_size=32)

Testing the RNN Model

It is always a good idea to run some simple checks to ensure our model is behaving as expected.

First, we can use the Model.summary function to print out a summary of the model’s internal workings. Here, we can inspect the layers in the model, the shape of the output of each of the layers, the batch size, etc.

Let’s run some simple checks to see if our model is behaving as expected.

First, we can use the Model.summary function to print out a summary of the model’s internal workings. Here, we can inspect the layers in the model, the shape of the output of each of the layers, the batch size, etc.

model.summary()

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 embedding (Embedding)       (32, None, 256)           21248     
                                                                 
 lstm (LSTM)                 (32, None, 1024)          5246976   
                                                                 
 dense (Dense)               (32, None, 83)            85075     
                                                                 
=================================================================
Total params: 5353299 (20.42 MB)
Trainable params: 5353299 (20.42 MB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________

1. 256 (Embedding Dimension):
   • Source: embedding_dim=256
   • Meaning: This is the output dimension of the embedding layer. The embedding layer converts each word (or character) in the vocabulary into a 256-dimensional dense vector. These vectors capture the relationships and meanings between words in the vocabulary.
2. 1024 (Number of LSTM Units):
   • Source: rnn_units=1024
   • Meaning: This is the number of units in the LSTM layer. The LSTM (Long Short-Term Memory) layer is the core of the model used to learn the temporal dependencies in the data. 1024 units mean that the LSTM layer outputs a 1024-dimensional vector at each time step. This high-dimensional space can capture complex patterns and dependencies.
3. 83 (Vocabulary Size or Number of Output Classes):
   • Source: vocab_size, used in model construction with len(vocab)
   • Meaning: This is the output dimension of the Dense layer and represents the total number of different characters (or words) that the model can recognize and generate. The Dense layer converts the LSTM layer’s output into final predictions, i.e., choosing a character from the vocabulary. 83 indicates the number of different characters the model can generate.

In summary, 256 is the output dimension of the embedding layer, representing the vectorized representation of each word; 1024 is the complexity of the LSTM layer, representing its ability to capture patterns in time-series data; 83 is the output size of the Dense layer, representing the number of different characters the model can generate.

We can also quickly check the dimensions of our output with a sequence length of 100. Note that this model can run on any length of input.

x, y = get_batch(vectorized_songs, seq_length=100, batch_size=32)
pred = model(x)
print("Input shape:      ", x.shape, " # (batch_size, sequence_length)")
print("Prediction shape: ", pred.shape, "# (batch_size, sequence_length, vocab_size)")

Input shape:       (32, 100)  # (batch_size, sequence_length)
Prediction shape:  (32, 100, 83) # (batch_size, sequence_length, vocab_size)

Untrained Model Predictions

Let’s see what our untrained model is predicting.

To get actual predictions from the model, we need to sample from the output distribution, defined over our character vocabulary with softmax. This will give us actual character indices. This means we use a categorical distribution to sample the example predictions. This gives the index of the predicted next character at each time step.

Note that we sample from this probability distribution instead of simply taking argmax, which can lead the model to get stuck in loops.

Let’s try this sampling for the first example in the batch.

sampled_indices = tf.random.categorical(pred[0], num_samples=1)
sampled_indices = tf.squeeze(sampled_indices,axis=-1).numpy()
sampled_indices

array([63,  5, 31, 39, 42, 40, 60, 38, 16, 68, 63, 26, 30, 15, 80, 72, 16,
       62, 29, 45, 58,  1, 22,  2,  2, 20, 18, 61, 61, 37, 64, 31, 22, 60,
       79, 26, 31, 30, 21, 80, 59, 42, 19, 52, 73, 23, 45, 12, 67, 35, 70,
        1, 32, 10, 37, 82, 27,  4, 13,  4, 67, 41, 65,  6, 62,  8, 78, 13,
        7,  1, 60, 69, 81,  2, 38, 77, 56, 49, 32, 62, 24, 56, 65, 20, 80,
       29, 63,  1, 14, 64, 75,  3, 82, 49, 55, 13, 51,  8, 68,  2])

We can now decode these predictions to see what the untrained model is predicting:

print("Input: \n", repr("".join(idx2char[x[0]])))
print()
print("Next Char Predictions: \n", repr("".join(idx2char[sampled_indices])))

Input: 
 'eaa egg|dBA ABd|eaa egg|dBG GBd|!\neaf g2e|dBA AGE|GAB dge|dBA A2:|!\n\nX:135\nT:Sean Bui\nZ: id:dc-jig-1'

Next Char Predictions:

 
 'h\'FNQOeM4mhAE3yq4gDTc :!!86ffLiF:exAFE9ydQ7[r<T0lJo G.L|B#1#lPj(g,w1) enz!MvaXGg=aj8yDh 2it"|X_1Z,m!'

As you can see, the text predicted by the untrained model is quite nonsensical! How can we do better? We can train the network!

Training the Model: Loss and Training Operations

It’s time to train the model!

At this point, we can treat the next character prediction problem as a standard classification problem. Given the previous state of the RNN and the input at a given time step, we want to predict the class of the next character - the actual next character prediction.

To train our model on this classification task, we can use a form of the crossentropy->cross-entropy loss (negative log-likelihood loss). Specifically, we will use sparse_categorical_crossentropy loss, as it uses integer targets for a multi-class classification task. We want to use the true targets - labels - and the predicted targets - logits - to compute the loss.

Let’s start by computing the loss for the example predictions from the untrained model:

### Defining the loss function ###

'''TODO: define the loss function to compute and return the loss between
    the true labels and predictions (logits). Set the argument from_logits=True.'''
# def compute_loss(labels, logits):
#   loss = tf.keras.losses.sparse_categorical_crossentropy('''TODO''', '''TODO''', from_logits=True) # TODO
#   return loss

def compute_loss(labels, logits):
  loss = tf.keras.losses.sparse_categorical_crossentropy(labels, logits, from_logits=True) # TODO
  return loss

'''TODO: compute the loss using the true next characters from the example batch
    and the predictions from the untrained model several cells above'''
# example_batch_loss = compute_loss('''TODO''', '''TODO''') # TODO

example_batch_loss = compute_loss(y, pred) # TODO

print("Prediction shape: ", pred.shape, " # (batch_size, sequence_length, vocab_size)")
print("scalar_loss:      ", example_batch_loss.numpy().mean())

Prediction shape:  (32, 100, 83)  # (batch_size, sequence_length, vocab_size)
scalar_loss:       4.4193177

Let’s start by defining some hyperparameters for training the model. We provide some reasonable values for the parameters initially. It’s up to you to use what we’ve learned in class to help optimize the parameter selection here!

### Hyperparameter setting and optimization ###

# Optimization parameters:
num_training_iterations = 4000  # Increase this to train longer
batch_size = 25  # Experiment between 1 and 64
seq_length = 200  # Experiment between 50 and 500
learning_rate = 5e-3  # Experiment between 1e-5 and 1e-1

# Model parameters:
vocab_size = len(vocab)
embedding_dim = 256
rnn_units = 1024  # Experiment between 1 and 2048

# Checkpoint location:
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "my_ckpt")

Now, we are ready to define our training operation - optimizer and training duration - and use this function to train the model. You will experiment with different optimizers and training durations to see how these changes affect the network’s output. Some optimizers you might try include Adam and Adagrad.

First, we instantiate a new model and an optimizer. Then, we will use the tf.GradientTape method to perform the backpropagation operation.

We will also generate a printout of the model’s training progress, which will help us easily see if we are minimizing the loss.

### Define optimizer and training operation ###

'''TODO: instantiate a new model for training using the `build_model`
  function and the hyperparameters created above.'''
model = build_model(
    vocab_size=vocab_size,
    embedding_dim=embedding_dim,
    rnn_units=rnn_units,
    batch_size=batch_size
    ) # TODO

'''TODO: instantiate an optimizer with its learning rate.
  Checkout the tensorflow website for a list of supported optimizers.
  https://www.tensorflow.org/api_docs/python/tf/keras/optimizers/
  Try using the Adam optimizer to start.'''
optimizer = tf.keras.optimizers.Adam(
    learning_rate=learning_rate,
    beta_1=0.9,
    beta_2=0.999,
    epsilon=1e-07,
    amsgrad=False,
    name='Adam',
    ) # TODO

@tf.function
def train_step(x, y):
  # Use tf.GradientTape()
  with tf.GradientTape() as tape:

    '''TODO: feed the current input into the model and generate predictions'''
    y_hat = model(x) # TODO

    '''TODO: compute the loss!'''
    loss = compute_loss(y, y_hat) # TODO

  # Now, compute the gradients
  '''TODO: complete the function call for gradient computation.
      Remember that we want the gradient of the loss with respect all
      of the model parameters.
      HINT: use `model.trainable_variables` to get a list of all model
      parameters.'''
  grads = tape.gradient(loss, model.trainable_variables) # TODO

  # Apply the gradients to the optimizer so it can update the model accordingly
  optimizer.apply_gradients(zip(grads, model.trainable_variables))
  return loss

##################
# Begin training!#
##################

history = []
plotter = mdl.util.PeriodicPlotter(sec=2, xlabel='Iterations', ylabel='Loss')
if hasattr(tqdm, '_instances'): tqdm._instances.clear() # clear if it exists

for iter in tqdm(range(num_training_iterations)):

  # Grab a batch and propagate it through the network
  x_batch, y_batch = get_batch(vectorized_songs, seq_length, batch_size)
  loss = train_step(x_batch, y_batch)

  # Update the progress bar
  history.append(loss.numpy().mean())
  plotter.plot(history)

  # Update the model with the changed weights!
  if iter % 100 == 0:
    model.save_weights(checkpoint_prefix)

print("Final Loss:", loss.numpy().mean())
# Save the trained model and the weights
model.save_weights(checkpoint_prefix)

In TensorFlow, model.trainable_variables is an attribute that contains all the trainable parameters in the model. These parameters are typically the weights and biases the model needs to learn, updated during the training process by optimization algorithms such as gradient descent.

The value returned by this attribute is a list, where each element is a TensorFlow variable (tf.Variable) representing a trainable parameter in the model.

In my code example:

grads = tape.gradient(loss, model.trainable_variables)

The tape.gradient function calculates the gradients of the loss function concerning each variable in model.trainable_variables. These gradients represent the local slopes of the loss function with respect to each parameter, indicating how to adjust these parameters to minimize the loss function.

In training neural networks, these gradients are crucial because they guide us on how to update the model’s weights to improve its predictions. In summary, model.trainable_variables is the collection of all parameters in the model that need to be learned through training, and tape.gradient is used in automatic differentiation to compute the gradients of these parameters, which is a key step in the model training process.

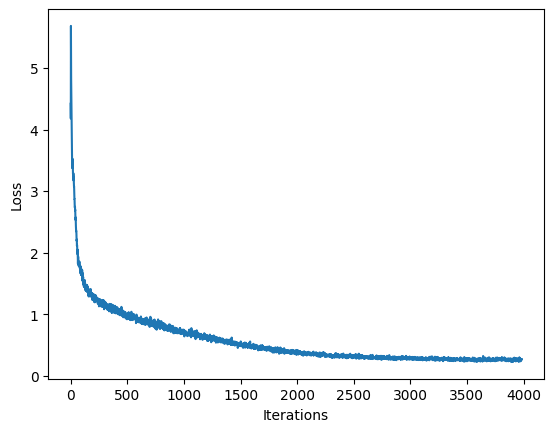
100%|██████████| 4000/4000 [05:58<00:00, 11.15it/s]
Final Loss: 0.27189144

Now, we can use our trained RNN model to generate some music! When generating music, we need to provide the model with some seed to start (since it cannot predict anything without an initial input!).

Generating Music with the RNN Model

Now, we can use our trained RNN model to generate some music! When generating music, we need to provide the

model with some seed to start (since it cannot predict anything without an initial input!).

Once we have a generated seed, we can iteratively predict each subsequent character using our trained RNN. Specifically, recall that our RNN outputs a softmax distribution over possible next characters. During inference, we iteratively sample from these distributions and use our samples to encode a generated song in ABC format.

Then all we have to do is write it to a file and listen!

Restoring the Latest Checkpoint

To make this inference step easy, we will use a batch size of 1. Since the RNN state is carried forward between time steps, once the model is built, it can only accept inputs of fixed batch size.

To run the model with a different batch_size, we need to rebuild the model and restore the weights from the latest checkpoint:

'''TODO: Rebuild the model using a batch_size=1'''
# model = build_model('''TODO''', '''TODO''', '''TODO''', batch_size=1)
model = build_model(vocab_size, embedding_dim, rnn_units, batch_size=1)

# Restore the model weights for the last checkpoint after training
model.load_weights(tf.train.latest_checkpoint(checkpoint_dir))
model.build(tf.TensorShape([1, None]))

model.summary()

Model: "sequential_2"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 embedding_2 (Embedding)     (1, None, 256)            21248     
                                                                 
 lstm_2 (LSTM)               (1, None, 1024)           5246976   
                                                                 
 dense_2 (Dense)             (1, None, 83)             85075     
                                                                 
=================================================================
Total params: 5353299 (20.42 MB)
Trainable params: 5353299 (20.42 MB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________

Notice that we input a fixed batch_size of 1 for inference.

The Prediction Procedure

Prediction Procedure Now, we are ready to write the code to generate music text in ABC notation:

• Initialize a "seed" starting string and RNN state, and set the number of characters we want to generate.
• Use the starting string and RNN state to get the probability distribution of the next predicted character.
• Sample from the multinomial distribution to compute the index of the predicted character. This predicted character is then used as the next input to the model.
• At each time step, the updated RNN state is fed back into the model, so it has more context when making the next prediction. After predicting the next character, the updated RNN state is fed back into the model, which is how it learns sequence dependencies in the data, as it gets more information from the previous predictions.

Complete and try out this code block (and some aspects of network definition and training!) to see how your model performs. How do songs generated after fewer training iterations compare to those generated after longer training?

### Prediction of a generated song ###

def generate_text(model, start_string, generation_length=1000):
  # Evaluation step (generating ABC text using the learned RNN model)

  '''TODO: convert the start string to numbers (vectorize)'''
  # input_eval = ['''TODO''']
  input_eval = [char2idx[s] for s in start_string]
  input_eval = tf.expand_dims(input_eval, 0)

  # Empty string to store our results
  text_generated = []

  # Here batch size == 1
  model.reset_states()
  tqdm._instances.clear()

  for i in tqdm(range(generation_length)):
      '''TODO: evaluate the inputs and generate the next character predictions'''
      # predictions = model('''TODO''')
      predictions = model(input_eval)

      # Remove the batch dimension
      predictions = tf.squeeze(predictions, 0)

      '''TODO: use a multinomial distribution to sample'''
      # predicted_id = tf.random.categorical('''TODO''', num_samples=1)[-1,0].numpy()
      predicted_id = tf.random.categorical(predictions, num_samples=1)[-1,0].numpy()

      # Pass the prediction along with the previous hidden state
      #   as the next inputs to the model
      input_eval = tf.expand_dims([predicted_id], 0)

      '''TODO: add the predicted character to the generated text!'''
      # Hint: consider what format the prediction is in vs. the output
      # text_generated.append('''TODO''')
      text_generated.append(idx2char[predicted_id])

  return (start_string + ''.join(text_generated))

'''TODO: Use the model and the function defined above to generate ABC format text of length 1000!
    As you may notice, ABC files start with "X" - this may be a good start string.'''
generated_text = generate_text(model, start_string="X", generation_length=1000) # TODO
# generated_text = generate_text('''TODO''', start_string="X", generation_length=1000)
generated_text

X:g__J_=ABcd cAFA|dDcD A,DFD|B,DFD B,DFD|B,DFD B,DFD|CEGE CDEC|!
D2FA D2FA|d2fd gdfd|edBd A2FA|B2AF GFED|!
fefg fefd|gfga g2fg|agbg agef|gedc BdAF|!
GABd g2fe|dedc Bcde|fece agae|cefe a3e|faec BABc:|!
A2cA eAcB|A2cA eAcB|ABcA BAFB|ABce fecA|BAcA BAFA|!
A2FA BAFA|A2FA BAFA|FABc dcdB|AFEF D2:|!

X:21
T:Fairies'
Z: id:dc-hornpipe-65
M:C|
L:1/8
K:F Major
eg|f2ec dcBA|a2fd Adfd|efed cABc|d2f2 d2:|!

X:27
T:Runch of Munster
Z: id:dc-slide-21
M:6/8
L:1/8
K:G Major
D|GFG BGB|d2B ABA|G2AG FGAB|cA=FA GABc|dgg2 agg2|d^cde fgag|fdcA dBcA:|!
[2 BAFA A2FA|Bged cbag|fedc Bged|(3cdc (3BcB A2ae|!
^cdef g2eg|f2df g2eg|fdec Adde|f3e defe|dBAF E2:|!

X:168
T:John Stenson's No. 1
Z: id:dc-reel-335
M:C
L:1/8
K:E Dorian
E|F2FE F2FE|D2FD ADFD|FABc dcdB|AFEF D3:|!
e|fded BAAB|d3f a3f|g2fg eBB2|dBAF BEE2:|!
Beef gfed|BdAF DEFe|afec Bafe|dBBA Bcde|[1 fde^c d2=cA|BdAG FDD2:|!
Add2 fdd2|fdgd add2|Add2 fdd2|aff2 dff2|dff2 dff2|dgg2 dff2|dff2 dff2|dgg2 d2:|!
fg|afdf a2gf|gfef gbag|faec dBAF|GFEF GABc|!
d2fd Adfd|defa

Play back the generated music!

We can now call a function to convert the ABC format text to an audio file and play it to listen to the generated music! If the resulting song is not long enough, try training for longer or regenerating the song!

### Play back generated songs ###

generated_songs = mdl.lab1.extract_song_snippet(generated_text)

for i, song in enumerate(generated_songs):
  # Synthesize the waveform from a song
  waveform = mdl.lab1.play_song(song)

  # If its a valid song (correct syntax), lets play it!
  if waveform:
    print("Generated song", i)
    ipythondisplay.display(waveform)

Found 3 songs in text
Generated song 1

Generated song 2

---

---

---

CN

Google Colab

引子

ABC记谱法：ABC notation

ABC记谱法是计算机记谱法的简写形式。在基本形式中，它使用带有 a-g、A-G 和 z 的字母符号来表示相应的音符和休止符，并使用其他元素来增加这些音符的附加值——升、降、升八度或降八度、音符长度、键和装饰。这种记谱形式开始于亥姆霍兹音高记谱法和使用ASCII字符模仿标准乐谱法（小节线、速度标记等）的结合，可以方便在线分享音乐，也为软件增加了一种新的、简单的语言开发人员，与其他为方便而设计的符号不同，例如指法和唱名法。

ABC记谱法包括音符、音长、调号、节拍等基本音乐元素的表示。下面是一个ABC记谱法的例子：

X:1
T:Alexander's
Z: id:dc-hornpipe-1
M:C|
L:1/8
K:D Major
(3ABc|dAFA DFAd|fdcd FAdf|gfge fefd|(3efe (3dcB A2 (3ABc|!
dAFA DFAd|fdcd FAdf|gfge fefd|(3efe dc d2:|!
AG|FAdA FAdA|GBdB GBdB|Acec Acec|dfaf gecA|!
FAdA FAdA|GBdB GBdB|Aceg fefd|(3efe dc d2:|!

这里的元素解释如下：

• X:1 - 这是曲目编号，表示这是集合中的第一首曲子。
• T:Alexander's - 这是曲目的标题，即“Alexander’s”。
• Z: id:dc-hornpipe-1 - 这是额外的标识信息，可能是用于某个数据库或集合中的唯一识别码。
• M:C| - 这定义了曲子的拍号。C|表示为“Cut time”（或 alla breve），这是2/2拍，一种常用于快速进行曲的拍号。
• L:1/8 - 这定义了默认的音符长度。这里是八分之一音符。
• K:D Major - 这指定了曲子的调号，即D大调。

接下来的部分是曲子的主要内容，使用特定的符号和字母表示音符和节奏：

• 括号中的数字和字母，如(3ABc，表示三连音。这意味着在通常的一个音符时值内演奏三个音符。
• 字母表示音符，大写字母表示低八度，小写字母表示高八度。例如，d和D分别表示高八度和低八度的D音。
• |用来表示小节的分隔。
• :用于标记乐句的结束，通常用于重复段落的结尾。

整个乐曲是一系列这样的音符和节奏模式的组合，构成了“Alexander’s”的旋律。这首曲子看起来是一首快节奏的舞曲，可能是一首hornpipe，这是一种在英国和爱尔兰流行的传统舞曲类型。

数据集

本实验中包含的所有数据集来自爱尔兰民歌，一共千余首，且都是有ABC记谱法表示的

# Download the dataset
songs = mdl.lab1.load_training_data()

# Print one of the songs to inspect it in greater detail!
example_song = songs[0]
print("\nExample song: ")
print(example_song)

Found 817 songs in text

Example song: 
X:1
T:Alexander's
Z: id:dc-hornpipe-1
M:C|
L:1/8
K:D Major
(3ABc|dAFA DFAd|fdcd FAdf|gfge fefd|(3efe (3dcB A2 (3ABc|!
dAFA DFAd|fdcd FAdf|gfge fefd|(3efe dc d2:|!
AG|FAdA FAdA|GBdB GBdB|Acec Acec|dfaf gecA|!
FAdA FAdA|GBdB GBdB|Aceg fefd|(3efe dc d2:|!

我们可以尝试用库函数来播放它

# Convert the ABC notation to audio file and listen to it
mdl.lab1.play_song(example_song)

通过引子，我们已经知道了，这种记谱法，包含音符信息的同时也包含了如歌曲题目、调式和节奏等元信息。文本文件中存在的不同字符数量如何影响学习问题的复杂度？当我们为文本数据生成数值表示时，这一点很快就会变得重要。

# Join our list of song strings into a single string containing all songs
songs_joined = "\n\n".join(songs)

# Find all unique characters in the joined string
vocab = sorted(set(songs_joined))
print(vocab)
print("There are", len(vocab), "unique characters in the dataset")

['\n', ' ', '!', '"', '#', "'", '(', ')', ',', '-', '.', '/', '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', ':', '<', '=', '>', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', '[', ']', '^', '_', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z', '|']
There are 83 unique characters in the dataset

我们可以看到组成所有元数据的独一无二的83个字符。

处理数据集

让我们退后一步，思考一下我们的预测任务。我们试图训练一个循环神经网络（RNN）模型来学习ABC记谱法中的音乐模式，然后使用这个模型基于所学的信息生成（即 predict）一首新的音乐作品。

具体来说，我们实际上是在问模型：给定一个字符或一系列字符，下一个最有可能的字符是什么？我们将训练模型来执行这个任务。

为了实现这一点，我们将一系列字符输入模型，并训练模型预测输出，即在每个 time step 的下一个字符。RNN保持一个取决于先前看到的元素的内部状态(internal state)，因此在生成预测时会考虑到直到给定时刻为止看到的所有字符的信息。

向量化文本

在开始训练我们的RNN模型之前，我们需要为我们的基于文本的数据集创建一个数值表示。为此，我们将生成两个查找表(lookup table)：一个将字符映射到数字，另一个将数字映射回字符。回想一下，我们刚刚确定了文本中存在的唯一字符。

### Define numerical representation of text ###

# Create a mapping from character to unique index.
# For example, to get the index of the character "d",
#   we can evaluate `char2idx["d"]`.
char2idx = {u:i for i, u in enumerate(vocab)}
print('{')
for char,_ in zip(char2idx, range(20)):
    print('  {:4s}: {:3d},'.format(repr(char), char2idx[char]))
print('  ...\n}')

# Create a mapping from indices to characters. This is
#   the inverse of char2idx and allows us to convert back
#   from unique index to the character in our vocabulary.
idx2char = np.array(vocab)
idx2char

我们可以 print 查看两者的内容

{
  '\n':   0,
  ' ' :   1,
  '!' :   2,
  '"' :   3,
  '#' :   4,
  "'" :   5,
  '(' :   6,
  ')' :   7,
  ',' :   8,
  '-' :   9,
  '.' :  10,
  '/' :  11,
  '0' :  12,
  '1' :  13,
  '2' :  14,
  '3' :  15,
  '4' :  16,
  '5' :  17,
  '6' :  18,
  '7' :  19,
  ...
}
array(['\n', ' ', '!', '"', '#', "'", '(', ')', ',', '-', '.', '/', '0',
       '1', '2', '3', '4', '5', '6', '7', '8', '9', ':', '<', '=', '>',
       'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M',
       'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z',
       '[', ']', '^', '_', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i',
       'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v',
       'w', 'x', 'y', 'z', '|'], dtype='<U1')

至此我们为每个字符提供了一个唯一的整数表示（即我们的词汇表），每个字符都被映射为从0到len(unique)的索引。

现在让我们正式实现将所有歌曲字符串转换为矢量化（即数字）表示

### Vectorize the songs string ###

'''TODO: Write a function to convert the all songs string to a vectorized
    (i.e., numeric) representation. Use the appropriate mapping
    above to convert from vocab characters to the corresponding indices.

  NOTE: the output of the `vectorize_string` function
  should be a np.array with `N` elements, where `N` is
  the number of characters in the input string
'''

def vectorize_string(string):
  output = [char2idx[char] for char in string]
  return np.array(output)
  # TODO

vectorized_songs = vectorize_string(songs_joined)
vectorized_songs

array([49, 22, 13, ..., 22, 82,  2])

我们还可以看看第一部分是如何被映射到整数表示的

print ('{} ---- characters mapped to int ----> {}'.format(repr(songs_joined[:10]), vectorized_songs[:10]))
# check that vectorized_songs is a numpy array
assert isinstance(vectorized_songs, np.ndarray), "returned result should be a numpy array"

nT:Alex' ---- characters mapped to int ----> [49 22 13  0 45 22 26 67 60 79]

创建训练样本和目标序列

我们的下一步是将文本划分为我们在训练中使用的 sample sequence（示例序列）。我们输入到RNN中的每个输入序列将包含来自文本的 seq_length 个字符。我们还需要为每个输入序列定义一个 target sequence（目标序列），这将用于训练RNN预测下一个字符。对于每个输入，相应的目标将包含相同长度的文本，只是向右移动了一个字符。

为此，我们将文本分割成 seq_length+1 的块。假设 seq_length 是4，我们的文本是 “Hello”。那么，我们的输入序列是 “Hell”，目标序列是 “ello”。

然后，batch method（批处理方法）将使我们能够将这些字符索引流转换为所需大小的序列。

### Batch definition to create training examples ###

def get_batch(vectorized_songs, seq_length, batch_size):
  # the length of the vectorized songs string
  n = vectorized_songs.shape[0] - 1
  # randomly choose the starting indices for the examples in the training batch
  # np.random.choice(a, size): 这个函数从0到a-1（包含0，不包含a）的整数中随机选取size个数。在这里，a 是n - seq_length，size是batch_size。
  idx = np.random.choice(n-seq_length, batch_size)

  '''TODO: construct a list of input sequences for the training batch'''
  input_batch = [vectorized_songs[i : i+seq_length] for i in idx]# TODO
  '''TODO: construct a list of output sequences for the training batch'''
  output_batch = [vectorized_songs[i+1 : i+seq_length+1] for i in idx]# TODO

  # x_batch, y_batch provide the true inputs and targets for network training
  x_batch = np.reshape(input_batch, [batch_size, seq_length])
  y_batch = np.reshape(output_batch, [batch_size, seq_length])
  return x_batch, y_batch


# Perform some simple tests to make sure your batch function is working properly!
test_args = (vectorized_songs, 10



             , 2)
if not mdl.lab1.test_batch_func_types(get_batch, test_args) or \
   not mdl.lab1.test_batch_func_shapes(get_batch, test_args) or \
   not mdl.lab1.test_batch_func_next_step(get_batch, test_args):
   print("======\n[FAIL] could not pass tests")
else:
   print("======\n[PASS] passed all tests!")

[PASS] test_batch_func_types
[PASS] test_batch_func_shapes
[PASS] test_batch_func_next_step
======
[PASS] passed all tests!

对于这些向量中的每一个，每个索引在单个 time step（时间步）被处理。因此，对于 time step 0 的输入，模型接收序列中第一个字符的索引，并尝试预测下一个字符的索引。在下一个 time step，它做同样的事情，但 RNN 除了当前输入外，还考虑了前一个步骤的信息，即其更新后的状态。

我们可以通过观察这在我们文本的前几个字符中是如何工作的来具体了解这一过程：

x_batch, y_batch = get_batch(vectorized_songs, seq_length=5, batch_size=1)

for i, (input_idx, target_idx) in enumerate(zip(np.squeeze(x_batch), np.squeeze(y_batch))):
    print("Step {:3d}".format(i))
    print("  input: {} ({:s})".format(input_idx, repr(idx2char[input_idx])))
    print("  expected output: {} ({:s})".format(target_idx, repr(idx2char[target_idx])))

Step   0
  input: 22 (':')
  expected output: 48 ('W')
Step   1
  input: 48 ('W')
  expected output: 60 ('e')
Step   2
  input: 60 ('e')
  expected output: 74 ('s')
Step   3
  input: 74 ('s')
  expected output: 75 ('t')
Step   4
  input: 75 ('t')
  expected output: 1 (' ')

The Recurrent Neural Network (RNN) model

现在我们准备好在我们的ABC记谱法音乐数据集上定义并训练一个RNN模型，然后使用这个训练好的模型生成一首新歌。我们将使用我们在前一部分生成的数据集中的歌曲片段批次来训练我们的RNN。

该模型基于LSTM（长短期记忆网络）架构，我们使用 state vector 来维持连续字符之间时间关系的信息。LSTM的最终输出然后被送入一个完全连接的Dense层，在这里我们将输出词汇表中每个字符上的softmax，然后从这个分布中采样以预测下一个字符。

此处的 softmax 指的是在神经网络的输出层使用的 softmax 激活函数。在训练语言模型（如此处的 RNN）时，softmax 函数通常被用于最后的 Dense 层，它将 LSTM 层的输出转换为实际的概率分布。

具体来说，softmax 函数的作用是：

1. 转换为概率：
   • 它接受任意实数值的向量（例如来自 Dense 层的原始输出或 logits）。
   • 然后，它将这些值映射到一组值上，这些值的范围在 0 到 1 之间，并且所有输出值的总和为 1。这意味着每个值都可以被解释为一个概率。这是一种归一化过程。
2. 多分类问题：
   • 在文本生成任务中，每个输出都对应于词汇表中的一个字符。
   • softmax 确保输出表示一个概率分布，其中每个字符的概率是根据模型的预测进行采样的可能性。
3. 采样：
   • 一旦有了这个概率分布，就可以从中采样来预测下一个字符。
   • 模型将选择概率最高的字符作为下一个字符，或者根据分布随机选择字符，以增加生成文本的多样性。

在我定义的模型中，每个时间步的 Dense 层的输出都会通过 softmax 函数，转换为词汇表中每个可能字符的概率。然后，基于这些概率，模型可以决定下一个最有可能的字符，或者根据这些概率随机抽取一个字符来生成文本。

正如我们在本实验室的第一部分中介绍的，我们将使用Keras API，具体来说是tf.keras.Sequential，来定义模型。用三层来定义模型：

• tf.keras.layers.Embedding：这是输入层，包含一个可训练的查找表，将每个字符的数字映射到一个具有 embedding_dim 维度的向量。
• tf.keras.layers.LSTM：我们的LSTM网络，大小为 units=rnn_units。
• tf.keras.layers.Dense：输出层，有 vocab_size 个输出。

现在，我们将定义一个函数，用来实际构建模型。

def LSTM(rnn_units):
  return tf.keras.layers.LSTM(
    rnn_units,
    return_sequences=True,
    recurrent_initializer='glorot_uniform',
    recurrent_activation='sigmoid',
    stateful=True,
  )

到了关键时刻！请填写 build_model 函数中的 TODOs 以定义RNN模型，然后调用你刚刚定义的函数来实例化模型！

### Defining the RNN Model ###

'''TODO: Add LSTM and Dense layers to define the RNN model using the Sequential API.'''
def build_model(vocab_size, embedding_dim, rnn_units, batch_size):
  model = tf.keras.Sequential([
    # Layer 1: Embedding layer to transform indices into dense vectors
    #   of a fixed embedding size
    tf.keras.layers.Embedding(vocab_size, embedding_dim, batch_input_shape=[batch_size, None]),

    # Layer 2: LSTM with `rnn_units` number of units.
    # TODO: Call the LSTM function defined above to add this layer.
    # LSTM('''TODO'''),
    LSTM(rnn_units),

    # Layer 3: Dense (fully-connected) layer that transforms the LSTM output
    #   into the vocabulary size.
    # TODO: Add the Dense layer.
    # '''TODO: DENSE LAYER HERE'''
    tf.keras.layers.Dense(vocab_size)
  ])

  return model

# Build a simple model with default hyperparameters. You will get the
#   chance to change these later.
model = build_model(len(vocab), embedding_dim=256, rnn_units=1024, batch_size=32)

测试 RNN 模型

运行一些简单的检查来确认我们的模型表现如预期总是一个好主意。

首先，我们可以使用 Model.summary 函数来打印出模型内部工作的概要。在这里，我们可以检查 the layers in the model, the shape of the output of each of the layers, the batch size, etc。

运行一些简单的检查来确认我们的模型表现是否如预期总是一个好主意。

首先，我们可以使用 Model.summary 函数来打印出模型内部工作的概要。在这里，我们可以检查模型中的层，每层的输出形状，批次大小等。

model.summary()

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 embedding (Embedding)       (32, None, 256)           21248     
                                                                 
 lstm (LSTM)                 (32, None, 1024)          5246976   
                                                                 
 dense (Dense)               (32, None, 83)            85075     
                                                                 
=================================================================
Total params: 5353299 (20.42 MB)
Trainable params: 5353299 (20.42 MB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________

1. 256 (嵌入维度):
   • 来源：embedding_dim=256
   • 意义：这是嵌入层（Embedding layer）的输出维度。嵌入层将词汇表中的每个词（或字符）转换为一个 256 维的密集向量。这些向量捕捉了词汇表中单词之间的关系和含义。
2. 1024 (LSTM单元数):
   • 来源：rnn_units=1024
   • 意义：这是 LSTM 层的单元数。LSTM（长短期记忆）层是模型的核心，用于学习数据中的时间依赖性。1024个单元意味着每个 time step（时间步长），LSTM层的输出是一个 1024 维的向量。这个高维空间可以捕获复杂的模式和依赖关系。
3. 83 (词汇表大小或输出类别数):
   • 来源：vocab_size，在模型构建时使用 len(vocab)
   • 意义：这是 Dense 层的输出维度，也是模型识别和生成的不同字符（或词汇）的总数。Dense层负责将 LSTM 层的输出转换为最终的预测，即从词汇表中选择一个字符。83表示模型在每个时间步可以选择的不同输出字符数。

简而言之，256是嵌入层的输出维度，表示每个词的向量化表示；1024是 LSTM 层的复杂度，表示其能力捕捉时间序列数据中的模式；83是 Dense 层的输出大小，表示模型可以生成的不同字符的数量。

我们还可以使用 100 的序列长度快速检查我们输出的维度。请注意，这个模型可以在任何长度的输入上运行。

x, y = get_batch(vectorized_songs, seq_length=100, batch_size=32)
pred = model(x)
print("Input shape:      ", x.shape, " # (batch_size, sequence_length)")
print("Prediction shape: ", pred.shape, "# (batch_size, sequence_length, vocab_size)")

Input shape:       (32, 100)  # (batch_size, sequence_length)
Prediction shape:  (32, 100, 83) # (batch_size, sequence_length, vocab_size)

未经训练的模型预测

让我们看看我们未训练的模型正在预测什么。

要从模型中获取实际预测，我们需要从输出分布中进行采样，这个输出分布是通过我们字符词汇的 softmax 定义的。这将给我们实际的字符索引。这意味着我们使用分类分布来对示例预测进行采样。这给出了在每个时间步骤中下一个字符（具体来说是其索引）的预测。

请注意，我们从这个概率分布中进行采样，而不是简单地取 argmax，这可能会导致模型陷入循环。

让我们尝试一下批次中第一个示例的这种采样。

sampled_indices = tf.random.categorical(pred[0], num_samples=1)
sampled_indices = tf.squeeze(sampled_indices,axis=-1).numpy()
sampled_indices

array([63,  5, 31, 39, 42, 40, 60, 38, 16, 68, 63, 26, 30, 15, 80, 72, 16,
       62, 29, 45, 58,  1, 22,  2,  2, 20, 18, 61, 61, 37, 64, 31, 22, 60,
       79, 26, 31, 30, 21, 80, 59, 42, 19, 52, 73, 23, 45, 12, 67, 35, 70,
        1, 32, 10, 37, 82, 27,  4, 13,  4, 67, 41, 65,  6, 62,  8, 78, 13,
        7,  1, 60, 69, 81,  2, 38, 77, 56, 49, 32, 62, 24, 56, 65, 20, 80,
       29, 63,  1, 14, 64, 75,  3, 82, 49, 55, 13, 51,  8, 68,  2])

我们现在可以解码这些预测，看看未训练模型预测的文本是什么样的：

print("Input: \n", repr("".join(idx2char[x[0]])))
print()
print("Next Char Predictions: \n", repr("".join(idx2char[sampled_indices])))

Input: 
 'eaa egg|dBA ABd|eaa egg|dBG GBd|!\neaf g2e|dBA AGE|GAB dge|dBA A2:|!\n\nX:135\nT:Sean Bui\nZ: id:dc-jig-1'

Next Char Predictions: 
 'h\'FNQOeM4mhAE3yq4gDTc :!!86ffLiF:exAFE9ydQ7[r<T0lJo G.L|B#1#lPj(g,w1) enz!MvaXGg=aj8yDh 2it"|X_1Z,m!'

正如你所看到的，未训练模型预测的文本是相当无意义的！我们怎样才能做得更好呢？我们可以训练这个网络！

Training the model: loss and training operations

现在是时候训练模型了！

在这一点上，我们可以将下一个字符的预测问题视为一个标准的分类问题。考虑到RNN的先前状态以及在给定时间步的输入，我们想要预测下一个字符的类别 —— 也就是实际预测下一个字符。

为了在这个分类任务上训练我们的模型，我们可以使用 crossentropy->交叉熵损失（负对数似然损失）的一种形式。具体来说，我们将使用sparse_categorical_crossentropy损失，因为它使用整数目标进行分类分类任务。我们会想要使用:真实目标 ——> labels —— 和预测目标 ——> logits —— 来计算损失。

让我们首先使用未训练模型的示例预测来计算损失：

### Defining the loss function ###

'''TODO: define the loss function to compute and return the loss between
    the true labels and predictions (logits). Set the argument from_logits=True.'''
# def compute_loss(labels, logits):
#   loss = tf.keras.losses.sparse_categorical_crossentropy('''TODO''', '''TODO''', from_logits=True) # TODO
#   return loss

def compute_loss(labels, logits):
  loss = tf.keras.losses.sparse_categorical_crossentropy(labels, logits, from_logits=True) # TODO
  return loss

'''TODO: compute the loss using the true next characters from the example batch
    and the predictions from the untrained model several cells above'''
# example_batch_loss = compute_loss('''TODO''', '''TODO''') # TODO

example_batch_loss = compute_loss(y, pred) # TODO

print("Prediction shape: ", pred.shape, " # (batch_size, sequence_length, vocab_size)")
print("scalar_loss:      ", example_batch_loss.numpy().mean())

Prediction shape:  (32, 100, 83)  # (batch_size, sequence_length, vocab_size)
scalar_loss:       4.4193177

让我们从为训练模型定义一些超参数开始。首先，我们提供了一些参数的合理值。由你来使用我们在课堂上学到的知识来帮助优化这里的参数选择！

### Hyperparameter setting and optimization ###

# Optimization parameters:
num_training_iterations = 4000  # Increase this to train longer
batch_size = 25  # Experiment between 1 and 64
seq_length = 200  # Experiment between 50 and 500
learning_rate = 5e-3  # Experiment between 1e-5 and 1e-1

# Model parameters:
vocab_size = len(vocab)
embedding_dim = 256
rnn_units = 1024  # Experiment between 1 and 2048

# Checkpoint location:
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "my_ckpt")

现在，我们准备好定义我们的训练操作——优化器和训练持续时间——并使用这个函数来训练模型。你将尝试使用不同的优化器和训练时长，看看这些改变如何影响网络的输出。你可能想尝试的一些优化器包括Adam 和 Adagrad。

首先，我们将实例化一个新模型和一个优化器。然后，我们将使用tf.GradientTape方法来执行反向传播操作。

我们还将生成一个模型训练进度的打印输出，这将帮助我们轻松地看到我们是否在 minimizing the loss。

### Define optimizer and training operation ###

'''TODO: instantiate a new model for training using the `build_model`
  function and the hyperparameters created above.'''
model = build_model(
    vocab_size=vocab_size,
    embedding_dim=embedding_dim,
    rnn_units=rnn_units,
    batch_size=batch_size
    ) # TODO

'''TODO: instantiate an optimizer with its learning rate.
  Checkout the tensorflow website for a list of supported optimizers.
  https://www.tensorflow.org/api_docs/python/tf/keras/optimizers/
  Try using the Adam optimizer to start.'''
optimizer = tf.keras.optimizers.Adam(
    learning_rate=learning_rate,
    beta_1=0.9,
    beta_2=0.999,
    epsilon=1e-07,
    amsgrad=False,
    name='Adam',
    ) # TODO

@tf.function
def train_step(x, y):
  # Use tf.GradientTape()
  with tf.GradientTape() as tape:

    '''TODO: feed the current input into the model and generate predictions'''
    y_hat = model(x) # TODO

    '''TODO: compute the loss!'''
    loss = compute_loss(y, y_hat) # TODO

  # Now, compute the gradients
  '''TODO: complete the function call for gradient computation.
      Remember that we want the gradient of the loss with respect all
      of the model parameters.
      HINT: use `model.trainable_variables` to get a list of all model
      parameters.'''
  grads = tape.gradient(loss, model.trainable_variables) # TODO

  # Apply the gradients to the optimizer so it can update the model accordingly
  optimizer.apply_gradients(zip(grads, model.trainable_variables))
  return loss

##################
# Begin training!#
##################

history = []
plotter = mdl.util.PeriodicPlotter(sec=2, xlabel='Iterations', ylabel='Loss')
if hasattr(tqdm, '_instances'): tqdm._instances.clear() # clear if it exists

for iter in tqdm(range(num_training_iterations)):

  # Grab a batch and propagate it through the network
  x_batch, y_batch = get_batch(vectorized_songs, seq_length, batch_size)
  loss = train_step(x_batch, y_batch)

  # Update the progress bar
  history.append(loss.numpy().mean())
  plotter.plot(history)

  # Update the model with the changed weights!
  if iter % 100 == 0:
    model.save_weights(checkpoint_prefix)

print("Final Loss:", loss.numpy().mean())
# Save the trained model and the weights
model.save_weights(checkpoint_prefix)

在TensorFlow中，model.trainable_variables 是一个属性，它包含了模型中所有可以训练的参数。这些参数通常是模型需要学习的权重和偏置，它们是模型在训练过程中通过优化算法（如梯度下降）更新的变量。

这个属性的返回值是一个列表，其中每个元素都是一个 TensorFlow 变量（tf.Variable），代表了模型中的一个可训练参数。

在我的代码示例中：

grads = tape.gradient(loss, model.trainable_variables)

tape.gradient 函数计算相对于model.trainable_variables中的每个变量的损失函数的梯度。这些梯度代表了损失函数相对于每个参数的局部斜率，它们指示了如何调整这些参数以最小化损失函数。

在训练神经网络时，这些梯度是非常重要的，因为它们告诉我们如何更新模型的权重来改进模型的预测。简而言之，model.trainable_variables 是模型中所有需要通过训练学习的参数的集合，而 tape.gradient 是在自动微分中用来计算这些参数的梯度的函数，这是模型训练过程的关键步骤。

100%|██████████| 4000/4000 [05:58<00:00, 11.15it/s]
Final Loss: 0.27189144

现在，我们可以使用我们训练好的RNN模型来生成一些音乐了！在生成音乐时，我们需要给模型提供某种种子以开始（因为没有初始输入，它无法进行任何预测！）。

使用 RNN 模型生成音乐

现在，我们可以使用我们训练好的RNN模型来生成一些音乐了！在生成音乐时，我们需要给模型提供某种 seed（种子）以开始（因为没有初始输入，它无法进行任何预测！）。

一旦我们有了一个生成的种子，我们就可以使用我们训练好的RNN迭代地预测每个后续字符（记住，我们使用ABC记谱法来表示我们的音乐）。更具体地说，回想一下我们的RNN输出可能的后续字符的 softmax 分布。在推理过程中，我们迭代地从这些分布中采样，然后使用我们的样本来编码一个用ABC格式表示的生成歌曲。

然后，我们所要做的就是将其写入文件并听听看！

恢复最新的检查点

为了使这个推理步骤简单，我们将使用批量大小为1。由于RNN状态是如何从一个时间步传递到下一个时间步的，一旦模型建立，它将只能接受固定的批量大小。

要在不同的 batch_size 下运行模型，我们需要重建模型并从最新的检查点恢复 weights，即在训练期间最后一个检查点之后的 weights：

'''TODO: Rebuild the model using a batch_size=1'''
# model = build_model('''TODO''', '''TODO''', '''TODO''', batch_size=1)
model = build_model(vocab_size, embedding_dim, rnn_units, batch_size=1)

# Restore the model weights for the last checkpoint after training
model.load_weights(tf.train.latest_checkpoint(checkpoint_dir))
model.build(tf.TensorShape([1, None]))

model.summary()

Model: "sequential_2"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 embedding_2 (Embedding)     (1, None, 256)            21248     
                                                                 
 lstm_2 (LSTM)               (1, None, 1024)           5246976   
                                                                 
 dense_2 (Dense)             (1, None, 83)             85075     
                                                                 
=================================================================
Total params: 5353299 (20.42 MB)
Trainable params: 5353299 (20.42 MB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________

请注意，我们在推理时输入了固定的 batch_size 为1。

The prediction procedure

预测过程 现在，我们准备好编写代码以ABC记谱法格式生成音乐文本：

• 初始化一个“seed”起始字符串和RNN state，并设置我们想要生成的字符数量。
• 使用起始字符串和RNN状态获得下一个预测字符的概率分布。
• 从多项分布中采样以计算预测字符的索引。这个预测的字符然后被用作模型的下一个输入。
• 在每个 time step，更新后的 RNN state 被反馈到模型中，因此它在进行下一个预测时具有更多的上下文。预测下一个字符后，更新后的RNN状态再次被反馈到模型中，这就是它如何在数据中学习 sequence dependencies 的方式，因为它从之前的预测中获取了更多信息。

完成并尝试这个代码块（以及网络定义和训练的一些方面！），看看模型的表现如何。在较少的训练周期之后生成的歌曲与经过较长时间训练之后生成的歌曲相比如何？

### Prediction of a generated song ###

def generate_text(model, start_string, generation_length=1000):
  # Evaluation step (generating ABC text using the learned RNN model)

  '''TODO: convert the start string to numbers (vectorize)'''
  # input_eval = ['''TODO''']
  input_eval = [char2idx[s] for s in start_string]
  input_eval = tf.expand_dims(input_eval, 0)

  # Empty string to store our results
  text_generated = []

  # Here batch size == 1
  model.reset_states()
  tqdm._instances.clear()

  for i in tqdm(range(generation_length)):
      '''TODO: evaluate the inputs and generate the next character predictions'''
      # predictions = model('''TODO''')
      predictions = model(input_eval)

      # Remove the batch dimension
      predictions = tf.squeeze(predictions, 0)

      '''TODO: use a multinomial distribution to sample'''
      # predicted_id = tf.random.categorical('''TODO''', num_samples=1)[-1,0].numpy()
      predicted_id = tf.random.categorical(predictions, num_samples=1)[-1,0].numpy()

      # Pass the prediction along with the previous hidden state
      #   as the next inputs to the model
      input_eval = tf.expand_dims([predicted_id], 0)

      '''TODO: add the predicted character to the generated text!'''
      # Hint: consider what format the prediction is in vs. the output
      # text_generated.append('''TODO''')
      text_generated.append(idx2char[predicted_id])

  return (start_string + ''.join(text_generated))

'''TODO: Use the model and the function defined above to generate ABC format text of length 1000!
    As you may notice, ABC files start with "X" - this may be a good start string.'''
generated_text = generate_text(model, start_string="X", generation_length=1000) # TODO
# generated_text = generate_text('''TODO''', start_string="X", generation_length=1000)
generated_text

X:g__J_=ABcd cAFA|dDcD A,DFD|B,DFD B,DFD|B,DFD B,DFD|CEGE CDEC|!
D2FA D2FA|d2fd gdfd|edBd A2FA|B2AF GFED|!
fefg fefd|gfga g2fg|agbg agef|gedc BdAF|!
GABd g2fe|dedc Bcde|fece agae|cefe a3e|faec BABc:|!
A2cA eAcB|A2cA eAcB|ABcA BAFB|ABce fecA|BAcA BAFA|!
A2FA BAFA|A2FA BAFA|FABc dcdB|AFEF D2:|!

X:21
T:Fairies'
Z: id:dc-hornpipe-65
M:C|
L:1/8
K:F Major
eg|f2ec dcBA|a2fd Adfd|efed cABc|d2f2 d2:|!

X:27
T:Runch of Munster
Z: id:dc-slide-21
M:6/8
L:1/8
K:G Major
D|GFG BGB|d2B ABA|G2AG FGAB|cA=FA GABc|dgg2 agg2|d^cde fgag|fdcA dBcA:|!
[2 BAFA A2FA|Bged cbag|fedc Bged|(3cdc (3BcB A2ae|!
^cdef g2eg|f2df g2eg|fdec Adde|f3e defe|dBAF E2:|!

X:168
T:John Stenson's No. 1
Z: id:dc-reel-335
M:C
L:1/8
K:E Dorian
E|F2FE F2FE|D2FD ADFD|FABc dcdB|AFEF D3:|!
e|fded BAAB|d3f a3f|g2fg eBB2|dBAF BEE2:|!
Beef gfed|BdAF DEFe|afec Bafe|dBBA Bcde|[1 fde^c d2=cA|BdAG FDD2:|!
Add2 fdd2|fdgd add2|Add2 fdd2|aff2 dff2|dff2 dff2|dgg2 dff2|dff2 dff2|dgg2 d2:|!
fg|afdf a2gf|gfef gbag|faec dBAF|GFEF GABc|!
d2fd Adfd|defa

Play back the generated music!

我们现在可以调用一个函数将ABC格式的文本转换成音频文件，然后播放它来听听我们生成的音乐！如果结果歌曲不够长，尝试更长时间的训练，或者重新生成歌曲！

### Play back generated songs ###

generated_songs = mdl.lab1.extract_song_snippet(generated_text)

for i, song in enumerate(generated_songs):
  # Synthesize the waveform from a song
  waveform = mdl.lab1.play_song(song)

  # If its a valid song (correct syntax), lets play it!
  if waveform:
    print("Generated song", i)
    ipythondisplay.display(waveform)

Found 3 songs in text
Generated song 1

Generated song 2