第二章 文法和语言
一些概念
语言
可以看成在一个基本符号集上定义的，按一定规则构成的一切基本符号串组成的集合
语法
指一组规则，用它可以形成和产生一个合适的程序
字母表（符号集）
—— 是一符号的非空有穷集合
—— 用 ∑、V 表示
符号串
符号的有穷序列。注意：ε 表示空符号串！
符号串集合
字母表 ∑ 上若干个符号串组成的集合
符号串运算
符号串相等：设 x 、y 是字母表 ∑ 上的两个符号串，若 x 与 y 的诸符号依次相等，则该两符号串相等，记为 x = y
符号串长度：设 x 是字母表 ∑ 上的符号串，符号串中包含符号的个数称为符号串 x 的长度，用 x 表示
e.g : (1). | ε | = 0 ; (2). | a x | = | x a | = | x | + 1 ( a ∈ ∑ )
符号串的连结：设 x 与 y 是字母表 ∑ 上的两个符号串，把 y 的所有符号相继写在 x 的符号之后所得到的符号串称为 x 与 y 的连结，用 xy 表示
注意**:**
- | x y | = | x | + | y |
- ε x = x ε = x
- x y ≠ y x ( 一般说来 )
符号串的逆：设 x 是字母表 ∑ 上的符号串，其逆为符号串 x 的倒置，记为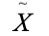 
。
e.g : (1). 若 x = abcd , 则 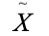= dcba (2). 
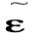= ε
符号串的前缀、后缀和子串：设 x、y、z 是字母表 ∑ 上的符号串，则称 x 为符号串 xy 的前缀，y 是符号 串 xy 的后缀， x、y 、 z 、xy 、yz 是符号串 x y z 的子串
e.g**: abcd**
符号串集合的乘积：设A、B为两个符号串集合，其乘积为 AB={xy|x∈A,y ∈B}
例**: (1).** 若 A = { ab, cd }, B = { ef, gh }
则**: AB ={ abef, abgh, cdef, cdgh }**
(2). ∵ εx = xε = x ∴ { ε } A = A { ε } = A
符号串的幂:设 x 是字母表 ∑ 上的符号串，则 x 的幂运算为 x 0 = ε x^1 = x x^2 = xx •••••• xx^n = x^n-1 x
e.g : 若 x = ab 则**: x^0** = ε**, x^1** = ab, x^2 = abab, ••••••,
x^n = abab••• ab
闭包，正闭包
集合 A 的闭包表示为 A*
正闭包表示为 A+
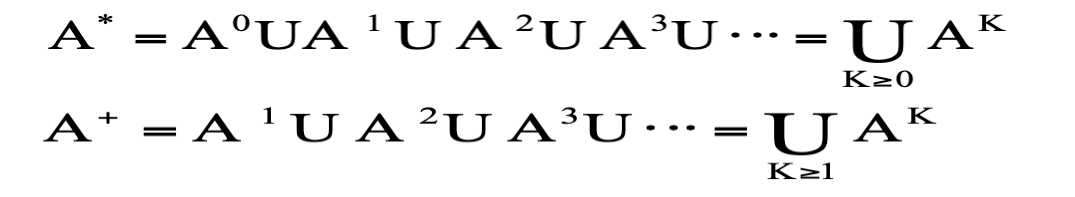
==注意==
空集
不含任何元素的集合，记为 Ø
注意**: (1). ØA = AØ = Ø ; (2).** ε ∉ Ø
推导
规约
注：用双箭头表示。
最右推导被称为规范推导，由规范推导所得的句型称为右句型或规范句型。
最右推导，最左规约。
句型,句子:
箭头注意是双箭头
重要约定
小写字母 a, b, c, ••• , r 表示符号
小写字母 s, t, u, ••• , z 表示符号串
大写字母 A, B, C, ••• , Z 表示符号串集合
文法的一些定义
文法的分类：
0型文法
1型文法
也叫上下文有关文法或长度增加文法。
2型文法
因为不用考虑上下文，非终结符可以直接替换
3型文法
正规文法
3型文法用来识别单词。2型文法用来识别句子。
- 文法实际使用的一些说明：
限制文法不得含有有害规则和多余规则。
一种题型：
将上下文无关文法改写为正规文法： 需要先写出语言，然后根据语言写出正规文法。
文法的化简：
- 消去p->p
- 消去不可达
- 消去无结果
语法树和文法二义性
短语等概念:
短语要经过一步推导
语法树层面：
短语：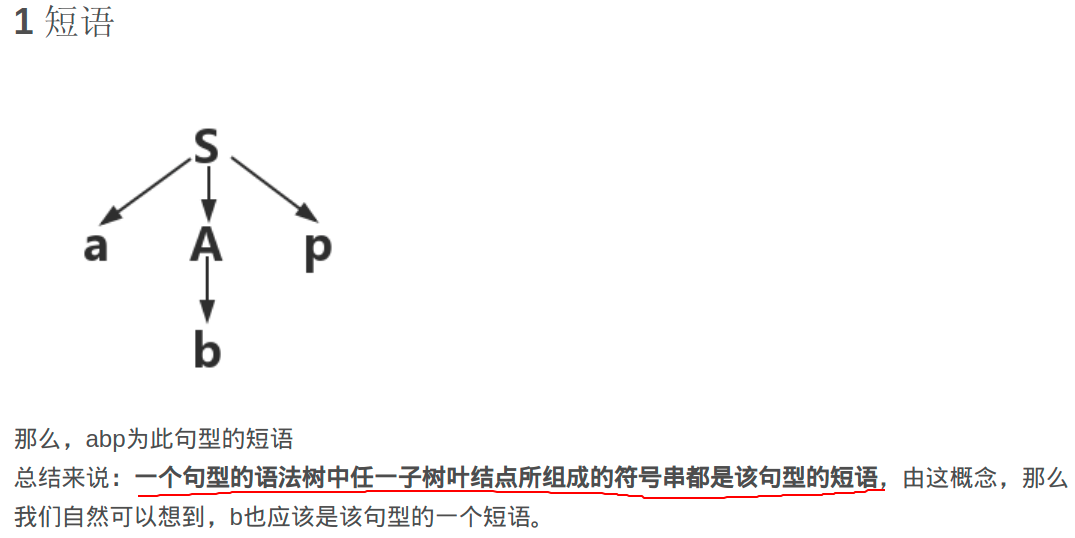
直接短语,简单短语
句柄
句柄就是句型中最左简单短语。句柄就是最左规约时要寻找的简单短语。
画语法树找短语。
例题：
语法树：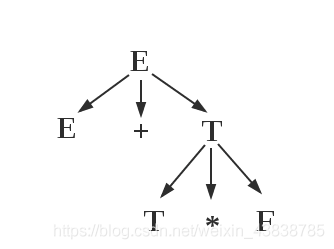
1 | 短语: T*F是相对于T的短语, E+T*F是相对于E的短语 |
二义性
文法的二义性和语言的二义性是两个不同的概念。
判断&证明：找一个例子，画出两棵语法树。
例题：
证明下面文法的二义性：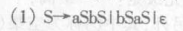
举反例方法，画推导的语法树时观察：
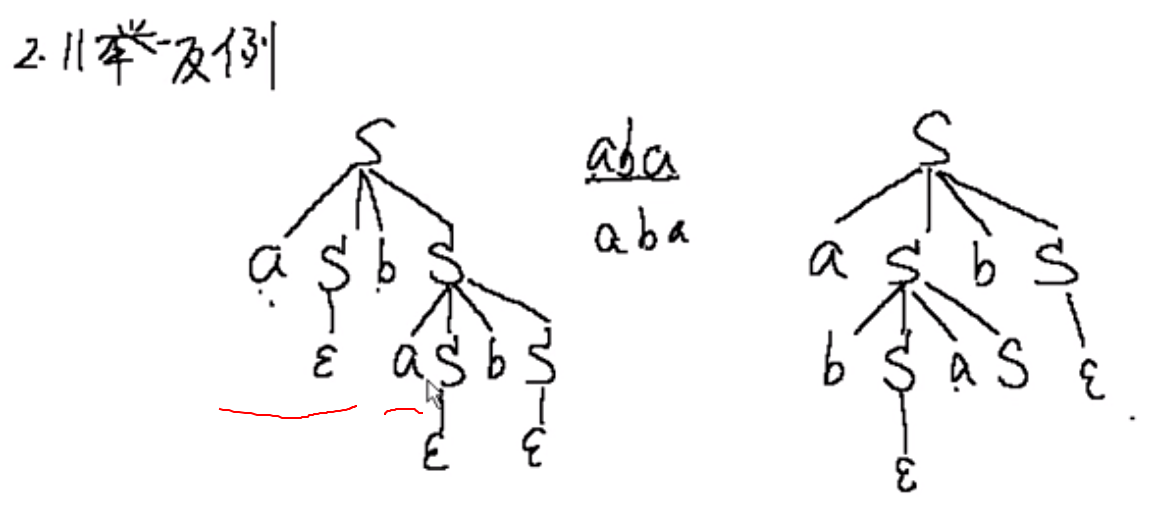
语言的二义性:
如果一个语言可以由不同文法来描述，那么这个语言是具有二义性的。特别地，如果所有能产生该语言的二型文法都是二义性文法，那么称这个语言是先天二义的。