盛最多水的容器

题目描述

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

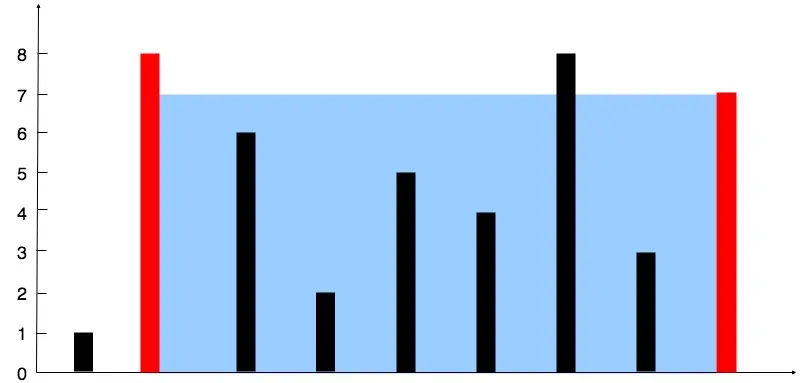
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/container-with-most-water
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

我的答案

func maxArea(height []int) int {
    // 双指针思想，找出最大 (indexr - indexp) * (height[indexr]>indexp[indexp]?indexp[indexp]:indexp[indexr])
    max := 0
    for p,r := 0,len(height)-1;p < r;{
        min := 0
        if height[p] > height[r]{
            min = height[r]
        }else{
            min = height[p]
        }
        if (r-p)*min > max{
            max = (r-p)*min
        }
        if height[p] > height[r]{
            r--
        }else{
            p++
        }
    }
    return max
}

个人觉得除了双指针没有更好的解法了。

解题思路

穷举法是O(n^2)的复杂度，会触发leetcode的时间限制。

O(n)的复杂度的解法是，保持两个指针 i , j ；分别指向长度数组的首尾。如果 ai 小于 aj ，则移动 i 向后（i++）。反之，移动 j 向前（j--）。如果当前的 area 大于了所记录的 area ，替换之。这个想法的基础是，如果 i 的长度小于 j ，无论如何移动 j ，短板在 i ，不可能找到比当前记录的 area 更大的值了，只能通过移动 i 来找到新的可能的更大面积。

更简练的描述如下：

• 若向内 移动短板 ，水槽的短板 min(h[i], h[j]) 可能变大，因此下个水槽的面积 可能增大 。

• 若向内 移动长板 ，水槽的短板 min(h[i], h[j]) 不变或变小，因此下个水槽的面积 一定变小 。

题解

func maxArea(height []int) int {
	// 从两端开始寻找，至少保证了宽度是最大值
	i, j := 0, len(height)-1
	max := 0

	for i < j {
		a, b := height[i], height[j]
		h := min(a, b)

		area := h * (j - i)
		if max < area {
			max = area
		}

		// 朝着area具有变大的可能性方向变化。
		if a < b {
			i++
		} else {
			j--
		}
	}

	return max
}

func min(i, j int) int {
	if i <= j {
		return i
	}
	return j
}

总结

• 双指针的妙用