快速排序 | 梧席

写在前面——关于快速排序，我其实很早就接触到了，但由于各种原因，始终都没有学，现在刚好在学 Java 的过程中碰到了，那就正好一并学一下。

快速排序（Quicksort）是对冒泡排序的一种改进，是一种排序执行效率很高的排序算法。

快速排序的基本思想时：通过一趟排序，将要排序的数据分隔成两个独立的部分，其中一部分的所以有数据比另外一部分所有数据都要小，然后按照此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此使整个数据变成有序序列。

具体的做法是：假设要对莫格元素进行排序，首先需要任意选取一个数据（通常选取第一个数据）作为关键数据，然后将所有比它小的数都放到它的前面，所有比它大的数都放到它的后面。这个过程称为一趟快速排序；递归调用此过程，即可实现数据的快速排序。

快速排序的Java具体实现

使用 Java 来对快速排序的具体实现如下：

（1）声明静态的 getMiddle() 方法，该方法需要返回一个 int 类型的参数值，在该方法中传入 3 个参数，代码如下：

public static int getMiddle(int[] list,int low,int high){
    int tmp = list[low]; // 数组第一个值作为中轴（分界点或关键数据）
    while(low < high){
        while(low < high && list[high] > tmp){
            high--;
        }
        list[low] = list[high]; // 比中轴小的记录移到低端
        while(low < high && list[low] < tmp){
            low++;
        }
        list[high] = list[low]; // 比中轴大的记录移到高端
    }
    list[low] = tmp; // 中轴记录到尾
    return low; // 返回中轴位置
}

（2）创建静态的 unckSort() 方法，在该方法中判断low参数是否小于high参数，如果是，则调用 getMiddle() 方法，将数组一分为二，并且调用自身方法进行递归排序。代码如下：

public static void unckSort(int[] list,int low,int high){
    if(low < high){
        int middle = getMiddle(list,low,high); // 将list数组一分为二
        unckSort(list,low,middle - 1); // 对低字表进行递归排序
        unckSort(list,middle + 1,high); // 对高字表进行递归排序
    }
}

（3）声明静态的 quick()方法，在该方法中判断传入的数组是否为空，弱国不为空，则调用 unckSort() 方法进行排序。代码如下：

public static void quick(int[] str){
    if(str.length > 0){
        // 查看数组是否为空
        unckSort(str,0,str.length - 1);
    }
}

（4）在 main() 方法中声明 int 类型的 number 数组，接着住处该数组的元素。然后调用自定义的 quick() 方法进行排序，排序后重新输出数组中的元素。代码如下：

int[] number = {13,15,24,99,14,11,1,2,3};
System.out.println("排序前：");
for(int val:number){
    System.out.print(val + " ");
}
quick(number);
System.out.println("排序后：");
for(int val:number){
    System.out.print(val + " ");
}

运行前面的代码进行测试，输出结果如下：

排序前：
13 15 24 99 14 11 1 2 3
排序后：
1 2 3 11 13 14 15 24 99

快速排序图解

假设有一组数列，初始值为 47，29，71，99，78，19，24，47

通过快速排序进行第 1 趟第 1 个交换的排序情况如下，第1次的操作情况如图 Quick-0 所示。

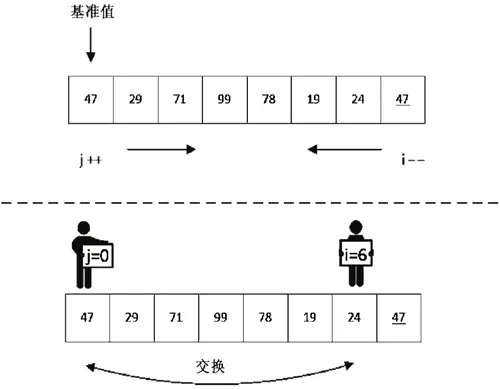
quick-0

交换之后，j 移动到了下标为 6 的位置，对 i 继续扫描，如图 Quick-1 所示。

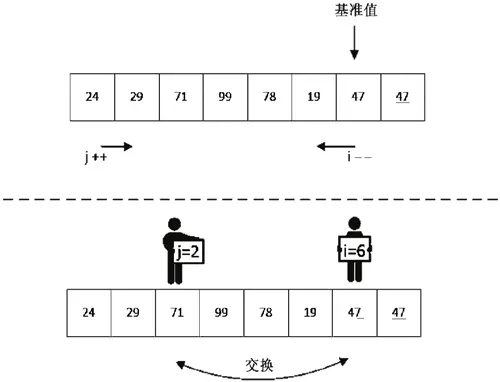
quick-1

此时交换后的数列变为 24、29、47、99、78、19、71、47。接下来我们继续对 i、j 进行操作，如图 Quick-2 所示，继续进行 i– 及 j++ 的比较操作。

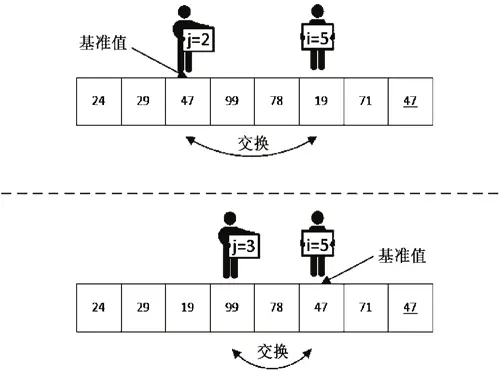
quick-2

进行了这两次 i、j 的移动、比较、交换之后，我们最终得到的数列是 24、29、19、47、78、99、71、47。接下来我们继续进行 i– 的操作，发现在 i 为 4 时比 47 大不用交换，在 i 为 3 时与 j 相遇，这时就不需要继续移动、比较了，已经找到 k 了，并且 k 的值为 3。我们可以确认一下当前的数列是不是 k 左边的值都比 47 小，而 k 右边的值都比 47 大（由于要保持相对位置不变，所以 47 同样在基准值 47 的右边）。

47 这个值已经落到了它该在的位置，第 1 趟排序完成了。接下来就是以 k 为基准，分为两部分，然后在左右两部分分别执行上述排序操作，最后数据会分为 4 部分；接着对每部分进行操作，直到每部分都只有一个值为止。

最终数列的结果是 19、24、29、47、47、71、78、99，怎么样，快速排序是不是非常简单地完成了所有的排序呢？虽然本次快速排序没有改变相同值的元素的顺序，但是由于快速排序需要对数列中的元素来回移动，有时还是会改变相对顺序的（比如 47 在第 1 轮的移动过程中就被移动到 47 的右边了），所以快速排序并不是一个稳定的算法。

快速排序的特点和性能

快速排序是在冒泡排序的基础上改进而来的，冒泡排序每次只能交换相邻的两个元素，而可快速排序则是跳跃式进行交换，交换的距离很大，因此总的比较和交换次数少了很多，速度也快了不少。

快速排序在最坏的情况下的时间复杂度和冒泡排序一样，是 O(n2) ，实际上每种比较都要交换的情况很少见。

快速排序只是使用数组原本的空间进行排序，所以所占用的空间是常量级的，但是由于每次划分之后是递归调用，所以递归调用在运行的过程中会消耗一定的空间，在一般情况下的空间复杂度为 O(logn) ，在最差的情况下，若每次只完成了一个元素，那么空间复杂度为 O(n) 。所以我们一般认为快速排序的空间复杂度为 O(logn)。

快速排序是一个不稳定的算法，在经过排序之后，可能会对相同值的元素的相对位置造成改变。

快速排序基本上被认为是相同数量级的所有排序算法中，平均性能最好的。